问题
计算题
（14分）如图所示，在竖直平面内，由斜面和圆形轨道分别与水平面相切连接而成的光滑轨道，圆形轨道的半径为R。质量为m的小物块从斜面上距水平面高为h=2.5R的A点由静止开始下滑，物块通过轨道连接处的B、C点时，无机械能损失。求：
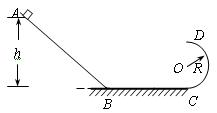
⑴.小物块通过B点时速度vB的大小；
⑵.小物块通过圆形轨道最低点C时轨道对物块的支持力N的大小；
⑶.小物块能否通过圆形轨道的最高点D。
答案
解：（1）物块从A点运动到B点的过程中，由动能定理得
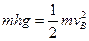（2分）
解得：
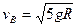（1分）
（2）物块从B至C做匀速直线运动
∴
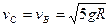（1分）
物块通过圆形轨道最低点C时，由牛顿第二定律有：
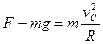（2分）
∴
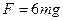（1分）
（3）若物块能从C点运动到D点，由动能定理得：
（2分）
解得：
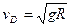（1分）
物块通过圆形轨道的最高点的最小速度为vD1，由牛顿第二定律得：
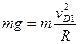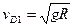（2分）
（2分）
可知物块能通过圆形轨道的最高点