如图所示,一位质量m="60" kg,参加“挑战极限运动”的业余选手,要越过一宽为s =" 2.5" m的水沟后跃上高为h="2.0" m的平台。他采用的方法是:手握一根长L="3.25" m的轻 质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的
质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的 顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)求:
顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计。(g取10m/s2)求:
(1)人要最终到达平台,在最高点飞出时刻的速度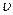 应至少
应至少 多大?
多大?
(2) 设人到达B点时速度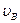 ="8" m/s ,人受的阻力为体重的0.1倍,助跑距离
="8" m/s ,人受的阻力为体重的0.1倍,助跑距离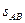 ="16" m ,则人在该过程中做的功为多少?
="16" m ,则人在该过程中做的功为多少?
(3)设人跑动过程中重心离地高度H="0." 8 m,在(1)、(2)两问的条件下,人要越过一宽为s =" 2.5" m的水沟后跃上高为h="2.0" m的平台,在整个过程中人应至少要做多少功?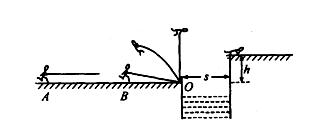
(1)设人开始做平抛运动时的最小速度为 ,则有
,则有
L一 h = 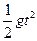 ……1分
……1分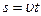 ……1分
……1分
 =" " 5 m/s ……1分
=" " 5 m/s ……1分
(2)由动能定理得:
W1— 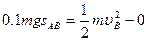 ……2分
……2分
W1 =" 2880" J……1分
(3)W2一mg(L一H) =  ……1分
……1分
据以上各式解得W2="300" J ……1分
W = W1 + W2 =" 3180" J ……1分
