问题
计算题
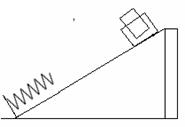
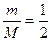如图所示为某探究活动小组设计的节能运动系统．斜面轨道倾角为30°，质量为M的木箱与轨道的动摩擦因数为
=
．木箱在轨道端时，自动装货装置将质量为m的货物装入木箱，然后木箱载着货物沿轨道无初速滑下，当木箱下滑L距离时，轻弹簧被压缩至最短，此时自动卸货装置立刻将货物卸下，然后木箱恰好被弹回到轨道顶端，再重复上述过程．(g取10m/s2)
求：（1）木箱不与弹簧接触时，木箱下滑的加速度与上滑的加速度
（2）此过程中弹簧最大的弹性势能.
（3）
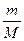比值为多少.
答案
（1）设下滑时加速度为a1,弹起离开弹簧后加速度为a2,则有
（M+m）gsin30°-
(M+m)gcos30°=（M+m）a1
解得：a1=2.5m/s2
Mgsin30°+Mgcos30°=Ma2
解得：a2=7.5m/s2
（2）弹簧最大的弹性势能为：W弹="M" gLsin30°+MgLcos30°
（3）在木箱与货物一起向下滑到卸货过程中，设弹力做功大小为W弹，
则有（M+m）gLsin30°-(M+m)gLcos30°-W弹=0
卸下货后，木箱被弹回轨道顶端，有
W弹-M gLsin30°-MgLcos30°=0
由以上解得：