如图所示，摩托车做腾跃特技表演，以1.0m／s的初速度沿曲面冲上高0.8m、顶部水平的高台，若摩托车冲上高台的过程中始终以额定功率1.8kW行驶，经过1.2s到达平台顶部，立即关闭油门，离开平台后，恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道，并沿轨道下滑．A、B为圆弧两端点，圆弧的最低点B与水平传送带相切,传送带以v1=8m/s的速度匀速运动,传送带长为8.5m，摩托车轮胎与传送带间为滑动摩擦,动摩擦因数为μ=0.4。已知圆弧半径为R=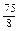
m，AB所对应的圆心角为θ=53o，人和车的总质量为180kg，特技表演的过程中到达传送带之前不计一切阻力(计算中取g=10m／s2，
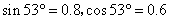)。求：
(1)人和车到达顶部平台时的速度v；
(2)从平台飞出到A点，人和车运动的水平距离s；
(3) 人和车运动到圆弧轨道最低点O时对轨道的压力；
(4) 人和车在传送带上的运动时间。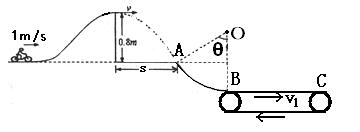
(1)摩托车冲上高台的过程中，由动能定理得
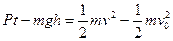………………………………………………①
代入数据解得
v=3m/s…………………………………………………………………………②
(2)摩托车离开平台后平抛运动过程中，在竖直方向
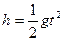……………………………………………………………………③
水平方向：
s=vt=1.2m………………………………………………………………………④
(3) 设人和车的最低点速度为vB,则摩托车由高台顶部到圆弧轨道最低点的过程中，
由机械能守恒定律得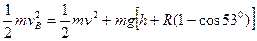
……………………⑤
得：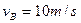
在最低点，据牛顿第二定律，有
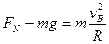……………………………………………………………⑥
代入数据解得
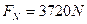
由牛顿第三定律可知，小孩对轨道的压力为
…………………………⑦
（4）由牛顿第二定律得：
……………………………………
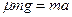………………………………⑧
解得：
由运动学公式得：
解得：
可知到达C点以前和传送带一起匀速运动。……⑨
再由运动学公式，得：
……………………………………………………………………⑩
解得：
………………………………………………………………………⑾
…………………………………………………………………………⑿
解得：
所以总时间为：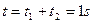
…………………………………………………⒀