问题
选择题
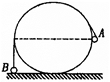
如图所示，A球质量为2m，B球质量为m，用不计质量不可伸长的绳子连接，并跨过固定在地面上的光滑圆柱，圆柱半径为R，A球恰好与圆柱中心等高，B球刚好接触地面，若将A球无初速释放，下列说法中正确的是（ ）
A.A球着地后，B球能上升到离地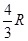
高度处
B.A球着地后，B球能上升到离地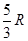
高度处
C.在A球着地前的任意时刻（除初始时刻外），A、B两球各自合力的功率之比为1∶1
D.在A球着地前的任意时刻（除初始时刻外），A、B两球各自合力的功率之比为2∶1
答案
AD
考点：
专题：机械能守恒定律应用专题．
分析：A、A球着地前，A、B两球组成的系统机械能守恒，根据系统机械能守恒，求出A球着地时，B球的速度，然后再单独对B球运用机械能守恒定律，求出B球还能上升的高度．
C、在A球着地前的任意时刻（除初始时刻外），两球的具有相同的速度大小和加速度大小，根据牛顿第二定律得出两球的合力之比，再根据P=F合v得出合力的功率之比．
解答：解：A、A球着地前，A、B两球组成的系统机械能守恒，有2mgR-mgR=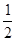
(2m+m)v2，得v=
．
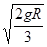A球着地后，B球做竖直上抛运动，设B球还能上升的高度为h，根据机械能守恒定律，有mgh=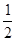mv2，得h=
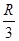．所以此时B球离地的高度H=
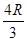．故A正确，B错误．
C、在A球着地前的任意时刻（除初始时刻外），两球的具有相同的速度大小和加速度大小，根据牛顿第二定律F合=ma，知两球所受的合力之比为2：1，再根据P=F合v，知合力的功率比为2：1．故C错误，D正确．
故选AD．
点评：解决本题的关键知道A球着地前，A、B因为除了受重力做功外，还有拉力做功，所以单个物体机械能不守恒，但系统机械能守恒．A球着地后，B球仅受重力，机械能守恒．