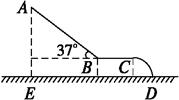
如图所示,为供儿童娱乐的滑梯的示意图,其中AB为斜面滑槽,与水平方向的夹角为θ=37°;长L的BC水平滑槽,与半径R=0.2m的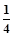 圆弧CD相切;ED为地面.已知儿童在滑槽上滑动时的动摩擦因数μ=0.5,在B点由斜面转到水平面的运动速率不变,A点离地面的竖直高度AE为H="2" m.(取g="10" m/s2,sin370=0.6, cos370=0.8)试求:
圆弧CD相切;ED为地面.已知儿童在滑槽上滑动时的动摩擦因数μ=0.5,在B点由斜面转到水平面的运动速率不变,A点离地面的竖直高度AE为H="2" m.(取g="10" m/s2,sin370=0.6, cos370=0.8)试求:
(1)儿童在斜面滑槽上滑下时的加速度大小?(要求作出儿童在斜面上运动时的受力分析图)
(2)儿童从A处由静止开始滑到B处时的速度大小?(结果可用根号表示)
(3)为了使儿童在娱乐时不会从C处平抛滑出,水平滑槽BC的长度L至少为多少?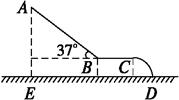
(14分)
(1)设儿童下滑的加速度大小为a,则有 受力分析图………………1分
mgsin37°-μmgcos37°=ma1 ①………………2分
解得:a1="2" m/s2. ②………………1分
(2)因为H="2" m,圆弧CD的半径R=0.8 m,
所以AB的长度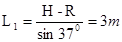 ③………………2分
③………………2分
设儿童滑到B点的速率为vB,则:vB2=2aL1, ④………………2分
(或依动能定理: 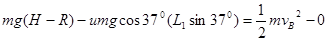 )
)
由②③④解得: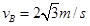 ⑤………………2分
⑤………………2分
(3)设儿童在C点恰做平抛运动滑出时的速率为vC,则: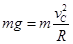 ⑥……1分
⑥……1分
f=umg=ma2 ⑦………………1分
-2a2L≤vC2-vB 2 ⑧………………1分
(或用动能定理: ……2分)
……2分)
由⑦⑧解得:L≥1 m.……1分
本题考查的是牛顿运动定律与圆周运动相结合的题。应用动能定理是本题最简便的方法,