问题
计算题
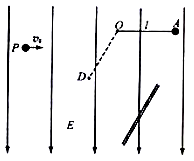
（2010·四川卷）25.（20分）如图所示，空间有场强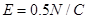
的竖直向下的匀强电场，长
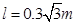的不可伸长的轻绳一端固定于O点，另一端系一质量
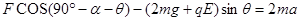的不带电小球
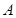，拉起小球至绳水平后，无初速释放。另一电荷量
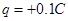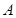、质量与相同的小球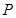
，以速度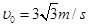
水平抛出，经时间
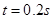与小球
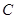与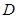
点下方一足够大的平板相遇。不计空气阻力，小球均可视为质点，取
。
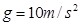（1）求碰撞前瞬间小球的速度。
（2）若小球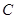经过路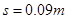
到达平板，此时速度恰好为0，求所加的恒力。
（3）若施加恒力后，保持平板垂直于纸面且与水平面的夹角不变，在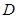点下方面任意改变平板位置，小球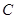均能与平板正碰，求出所有满足条件的恒力。
答案
（1）
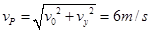（2）
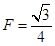α=30°（3）
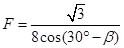（其中0≤β＜120°）
（1）P做抛物线运动，竖直方向的加速度为
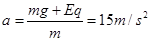
在D点的竖直速度为
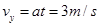
P碰前的速度为
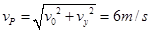
（2）设在D点轻绳与竖直方向的夹角为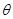
，由于P与A迎面正碰，则P与A速度方向相反，所以P的速度与水平方向的夹角为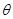有
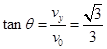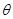，=30°
对A到达D点的过程中根据动能定理
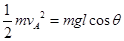
化简并解得
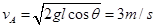
P与A迎面正碰结合为C，根据动量守恒得
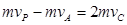
解得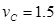 
m/s
小球C经过s速度变为0，一定做匀减速运动，根据位移推论式
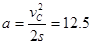m/s2
设恒力F与竖直方向的夹角为α，如图，根据牛顿第二定律
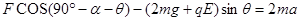
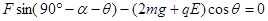
给以上二式带入数据得
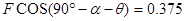
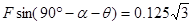
解得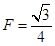 α=30°
（3）平板足够大，如果将平板放置到无限远根据题意也能相碰，此时小球C必须匀速或加速不能减速，所以满足条件的恒力在竖直线与C的速度线之间，设恒力与竖直方向的夹角为β，则 0≤β＜120°
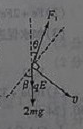
在垂直速度的方向上，恒力的分力与重力和电场力的分力等大反向，有
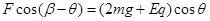
则满足条件的恒力为
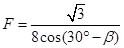（其中0≤β＜120°）