问题
计算题
如图所示，一水平传送带始终保持着大小为v＝4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道，其半径为R=0.2m，半圆弧形轨道最低点与传送带右端B衔接并相切，一小物块无初速地放到皮带左端A处，经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时，物块至最高点对轨道的压力为零，（g=10m/s2）则：
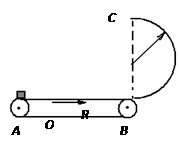
（1）物块至最高点C的速度为多少?
（2）物块在B点的速度为多少?物块与皮带间的动摩擦因数为多少？
（3）若只改变传送带的长度，使滑块滑至圆弧轨道的最高点C时对轨道的压力最大，传送带的长度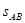
应满足什么条件？
答案
（1）
m/s（2）
（3）
≥1.6 m
（1）设小物块质量为m,至最高点C的速度为v
（2分） m/s（2分）
（2）从B到C过程中，
（2分）
m /s（2分）
从A到B的过程中
（2分） （2分）
（3）设刚好到达B点的最大速度为4 m /s（1分）
设AB之间的长度为
（1分） 
m
≥1.6 m（1分）
本题考查圆周运动规律，在最高点由重力提供向心力，列式求解，从B到C过程中，由动能定理可求出B点速度，再由传送带的摩擦力做功求得动摩擦因数
