(14分)如图所示,倾角θ = 60°的粗糙平直导轨与半径为R的光滑圆环轨道相切,切点为B,轻弹簧一端固定,自由端在B点,整个轨道处在竖直平面内。现将一质量为m的小滑块(视为质点)紧靠且压缩弹簧,并从导轨上离水平地面高h = 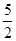 R的A处无初速下滑进入圆环轨道,恰能到达圆环最高点D,不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5,重力加速度大小为g。求:
R的A处无初速下滑进入圆环轨道,恰能到达圆环最高点D,不计空气阻力。滑块与平直导轨之间的动摩擦因数μ = 0.5,重力加速度大小为g。求:
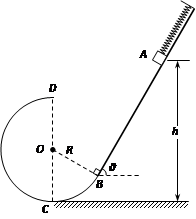
(1)滑块运动到圆环最高点D时速度υD的大小;
(2)滑块运动到圆环最低点时受到圆环轨道支持力N的大小;
(3)滑块在A处时弹簧的弹性势能Ep。
(1)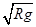 (2)N = 6mg (2)
(2)N = 6mg (2)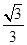 mgR
mgR
(1)滑块恰能到达圆环最高点D,说明滑块在D点时重力恰好提供向心力,即
mg = m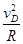 2分
2分
得 υD = 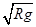 1分
1分
(2)小滑块从C→D,由机械能守恒定律得
 mυC2 =
mυC2 =  mυD2 + mg·2R 2分
mυD2 + mg·2R 2分
υC = 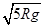 1分
1分
在C点,根据牛顿第二定律,有
N– mg = m 2分
2分
得 N = 6mg 1分
(2)AB之间长度
L = [h–(R– Rcosθ)]/sinθ=  R 1分
R 1分
平直导轨对滑块的滑动摩擦力
f = μmgcosθ = 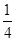 mg 1分
mg 1分
从A→C,根据能量守恒定律有
 mυC2 + fL = Ep + mgh 2分
mυC2 + fL = Ep + mgh 2分
得 Ep = 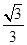 mgR 1分
mgR 1分
本题考查圆周运动规律的应用,在最高点通过的临界条件是只有重力提供向心力,从C到D可通过机械能守恒定律求得C点速度,在C点由支持力和重力的合力提供向心力,列式求解可得,在A到B间,通过动能定理可求得势能大小
