如图半径分别为2R和R的甲、乙两光滑圆形轨道固定放置在同一竖直平面内,两轨道之间由一条水平轨道CD相连,曲面轨道与水平面轨道在B处光滑连接(物块经过B点时没有机械能损失),现有一小物块从斜面上高h处的A点由静止释放,曲面轨道以及水平轨道BC段是光滑的,小物块与CD段以及D右侧的水平轨道间的动摩擦因数均为μ。已知小物块通过甲轨道最高点时与轨道间压力为物块重力的3倍,而后经过有摩擦的CD段后又进入乙轨道运动。
(1)求初始释放物块的高度h
(2)为避免出现小物块脱离圆形轨道乙而发生撞轨现象,则CD段的长度应满足什么条件?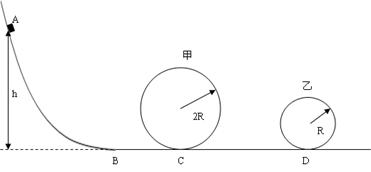
(1)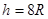 (2)
(2)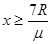
(1)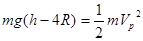 ---------- ①
---------- ①
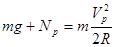 ---------- ②
---------- ②
已知 
得 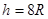 ---------- ③
---------- ③
(2)若能通过最高点有:
 ---------- ④
---------- ④
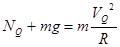 ---------- ⑤
---------- ⑤
因为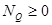 所以有
所以有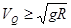 ---------- ⑥
---------- ⑥
得
得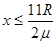 ---------- ⑦
---------- ⑦
若不能到达圆心对应的水平线以上,则速度可减小到零,设能上升的高度为h’,有: ---------- ⑧
---------- ⑧
 ---------- ⑨
---------- ⑨
得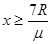 ---------- ⑩
---------- ⑩
评分细则:①④⑦⑧⑩各2分,②③⑤⑥⑨各1分,共15分。
本题考查动能定理和圆周运动,从最高点到达甲的最高点,由动能定理(只有重力做功)可求得在最高点的速度大小,在最高点由重力和弹力的合力提供向心力,列公式求解,在第二问中,通过最高点的最小速度是只有重力提供向心力,设此时距离为x,根据动能定理列出到达最高点动能的公式,只有重力提供向心力,由此可求得速度大小,再由动能定理求得距离x表达式,求解不等式皆可
