问题
计算题
（15分）如图所示，水平面上有一质量为m的平板B，平板左端放置一质量为2m的小物块A（可视为质点），A与B之间、B与水平面之间的动摩擦因数均为μ．开始时将一大小为6μmg（g为重力加速度）、方向水平向右的推力F1作用到平板上，使B和A一起从静止开始向右运动．当B运动的距离为x时，立刻将力F1撤去，同时将另一大小为3μmg、方向水平向右的推力F2作用到物块A上，经过一段时间物块脱离平板，此时物块A的速度大小为v．
（1）求力F1撤去的瞬间，平板B的速度．
（2）求从力F2开始作用至物块脱离平板的过程，物块A相对于地面的位移．
（3）试讨论平板的长度L与x和v之间的关系．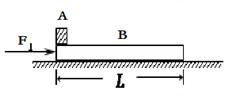
答案
(1)
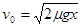(2)
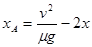(3)
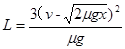
题目分析：（1）A、B 一起加速过程，由动能定理得
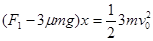
将F1=6μmg代入解得平板B的速度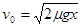
（2）从力F2作用到A上到A脱离平板过程，对A，由动能定理得
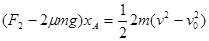
将F2=3μmg代入解得物块A相对于地面的位移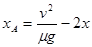
（3）作用力变化后，A 作匀加速运动，而B作匀减速运动直到停下。在B停下之前，系统所受外力的合力为0，动量守恒。
若A脱离B时，B恰好停下，由动量守恒定律得
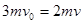⑤ 解得A的速度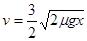
讨论：
①若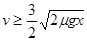
，则A脱离B时B已停下
对B，由动能定理得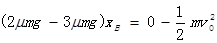 
平板长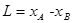
解得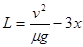
②若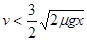
，则A脱离B时B未停下
由动量守恒定律得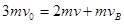 
对B，由动能定理得
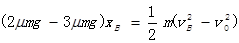
平板长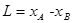 解得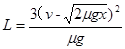
点评：做此类型的题目最注重过程，关键是弄清楚物体的运动变化
