问题
计算题
（10分）．如图所示，水平轨道AB与位于竖直面内半径为R="0.90" m的半圆形光滑轨道BCD相连，半圆形轨道的BD连线与AB垂直．质量为m=1.0kg可看作质点的小滑块在恒定外力F作用下从水平轨道上的A点由静止开始向右运动，物体与水平地面间的动摩擦因数μ=0.5．到达水平轨道的末端B点时撤去外力，小滑块继续沿半圆形轨道运动，且恰好能通过轨道最高点D，滑块脱离半圆形轨道后又刚好落到A点．g取10 m/s2，求：
（1）滑块经过B点进入圆形轨道时对轨道的压力大小
（2）滑块在AB段运动过程中恒定外力F的大小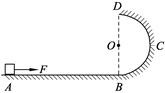
答案
（1）60 N，方向竖直向上（2）F="17.5" N
题目分析：（1）（5分）小滑块恰好通过最高点，则有：mg=m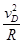
设滑块到达B点时的速度为vB，滑块由B到D过程由动能定理有： -2mgR=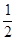
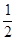mv2D-mv2B
对B点：FN-mg=m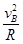
代入数据得：FN="60" N
由牛顿第三定律知滑块对轨道的压力为60 N，方向竖直向上
（2）（5分）滑块从D点离开轨道后做平抛运动，则：2R=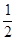gt2 SAB=vDt
滑块从A运动到B有：v2B=2aSAB 由牛顿第二定律有：F-μmg="ma"
代入数据得：F="17.5" N
点评：在圆周运动中，分为“有支撑物、无支撑物”两个模型，本题中在最高点D为无支撑物，明确刚好通过最高点是只有重力提供向心力