问题
计算题
(12分)如图所示，长为R的轻绳一端固定于O点，另一端拴一质量为m的小球，把球拉至最高点A，然后以υ0=
的水平速度抛出。
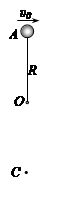
计算：（1）绳被拉直时小球的位置在何处？
（2）小球经过最低点C时小球对绳的拉力F？（设绳被拉直后小球沿绳方向的分速度迅速变为零）
（3）小球在整个运动过程中绳子对小球所做的功是多少？
答案
（1）小球运动到与O点在同一水平线上B点时绳恰好张紧（2）5mg（3）-0.25mgR
题目分析：（1）小球在最高点作圆周运动的最小速度应满足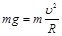 
解得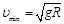
因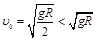
所以小球做平抛运动
设绳被拉直时小球所处的位置为B，绳与水平方向夹角为θ，如图甲所示 ，根据平抛运动规律有
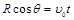
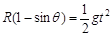
解得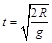
，θ=0º即小球运动到与O点在同一水平线上B点时绳恰好张紧，如图乙所示
（2）由于绳被拉直后小球沿绳方向的分速度迅速变为零，小球到达B点后，只剩竖直方向的速度vy了，且vy=gt=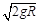
小球由B到C过程中机械能守恒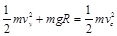 
解得 
在最低点C根据牛顿第二定律有 F–mg =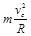
解得 F=5mg
根据牛顿第三定律，小球对绳子的拉力大小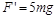
（3）小球从A到B再到C全程应用动能定理得
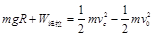
将vc、v0表达式代入解得绳子对小球所做的功 
点评：本题是动能定理和圆周运动的综合问题，考查学生对多过程问题的分析能力，通过对圆周运动的最高点临界速度可判断物体做平抛运动，利用运动的分解求得分速度大小，把整个运动过程分成若干个可独立的分运动，利用机械能守恒、动能定理或圆周运动求解