问题
计算题
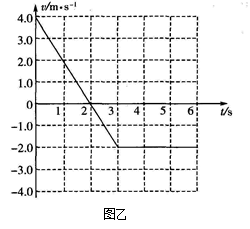
（19分）一足够长的水平传送带以恒定的速度运动，现将质量为M =2.0kg的小物块抛上传送带，如图甲所示。地面观察者记录了小物块抛上传送带后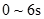
内的速度随时间变化的关系，以水平向右的方向为正方向，得到小物块的v-t 图像如图乙所示。取
。
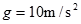(1)指出传送带速度的大小和方向；
(2)计算物块与传送带间的动摩擦因数μ；
(3)计算0-6s内传送带对小物块做的功；
(4)计算0-6s内由于物块与传送带摩擦产生的热量。
答案
(1)
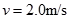(2)0.2(3)-12J(4)36J
题目分析：（1）由图可知传送带的速度大小为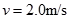，方向水平向左。（2分）
（2）由速度图象可得，物块在滑动摩擦力的作用下做匀变速运动的加速度为
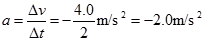（2分）
由牛顿第二定律得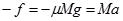 
（2分）
得物块与传送带间的动摩擦因数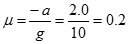 
（1分）
（3）根据动能定理，传送带对小物块做的功为
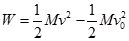（3分）
即 
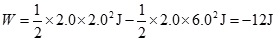（2分）
（4）物块从冲上传送带到相对静止的过程中，物块相对于传送带的速度为
（2分）
这个过程中，物块相对传送带的位移为
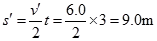（2分）
因摩擦而产生的热量为 
（3分）
点评：本题难度中等，利用动能定理求解问题时只需要确定初末状态，求解系统产生的热量时用到“相互作用力乘以相对位移”，也就是系统机械能的损失