问题
选择题
一个小物块从斜面底端冲上足够长的斜面后又返回到斜面底端，已知小物块的初动能为E，它返回到斜面底端的速度为v，克服摩擦力做功为E/2，若小物块以2E的初动能冲上斜面，则有( )
①返回斜面底端时的动能为3E/2
②返回斜面底端时的动能为E
③返回斜面底端时的速度大小为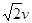
④小物块两次往返克服摩擦力做功相同
A．①④正确
B．②③ 正确
C．① ③正确
D．只有② 正确
答案
答案：B
题目分析：（1）冲上斜面和返回到斜面底端两过程中克服摩擦阻力做功相等；
（2）初动能增大后，上升的高度也随之变大，可根据匀减速直线运动的速度位移公式求出上升的位移，进而表示出克服摩擦力所做的功；
（3）对两次运动分别运用动能定理即可求解．
解：以初动能为E冲上斜面并返回的整个过程中运用动能定理得：
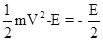①
设以初动能为E冲上斜面的初速度为V0，则以初动能为2E冲上斜面时，初速度为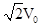
，加速度相同，
根据2ax=V2-V02可知第二次冲上斜面的位移是第一次的两倍，所以上升过程中克服摩擦力做功是第一次的两倍，整个上升返回过程中克服摩擦力做功是第一次的两倍，即为E．
以初动能为2E冲上斜面并返回的整个过程中运用动能定理得：
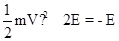②，
所以返回斜面底端时的动能为E，故A错误，B正确；
C、由①②得：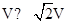
，故C正确，
D、第二次冲上斜面的位移是第一次的两倍，
所以上升过程中克服摩擦力做功是第一次的两倍，整个上升返回过程中克服摩擦力做功是第一次的两倍，故D错误．
故选B．
点评：本题难度较大．考查功能关系．该题考查了动能定理的直接应用，注意以不同的初动能冲上斜面时，运动的位移不同，摩擦力做的功也不同．