问题
计算题
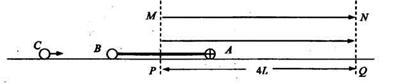
如图所示，在一绝缘粗糙的水平桌面上，用一长为2L的绝缘轻杆连接两个完全相同、 质量均为m的可视为质点的小球A和B球带电量为+q, B球不带电.开始时轻杆的中垂 线与竖直虚线MP重合，虚线NQ与MP平行且相距4L.在MP、NQ间加水平向右、电场强 度为E的匀强电场，AB球恰能静止在粗糙桌面上。取最大静摩擦力等于滑动摩擦力。求：
（1）A，B球与桌面间的动摩擦因数
(2) 若A球带电量为+8q时，S球带电量为-8q，将AB球由开始位置从静止释放，求A 球运动到最右端时拒虚线NQ的距离d,及AB系统从开始运动到最终静止所运动的总路程s:
(3) 若有质量为km、带电量为-k2q的C球，向右运动与B球正碰后粘合在一起，为 使A球刚好能到达虚线NQ的位置，问k取何值时，C与B碰撞前瞬间C球的速度最小？ C球速度的最小值为多大？（各小球与桌面间的动摩擦因数都相同。）
答案
（1）
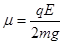（2）S=8L（3）当
，
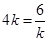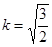时，v0有最小值v0min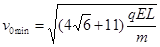 
题目分析：（1）以AB球整体为对象，处于静止状态，则有
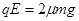则：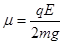
（2）从静止开始至A球运动到最右端的过程中电场力对A球作功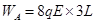
电场力对B球作负功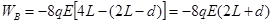
摩擦力对AB系统作负功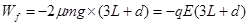
由动能定理可知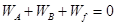
得：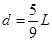
分析运动过程后可知，AB系统最终静止在电场中，对全程应用动能定理可得
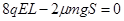则：S="8L"
（3）C与B球碰后，C与AB系统共同速度设为v1，由动量守恒可知
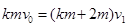
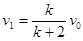
C与球碰后至A滑到虚线NQ位置过程中，由动能定理可知
由上面三式联立得
当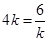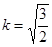，时，v0有最小值v0min
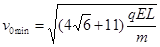
点评：本题结合了动能定理、动量守恒定律来研究多过程物理问题。在多过程物理问题时，应优先考虑能量或者动量观点。在处理问题时要注意动量守恒有成立条件，看看问题是否满足要求。