问题
解答题
点P在锐角△ABC的边上运动,试确定点P的位置,使PA+PB+PC最小,并证明你的结论.
答案
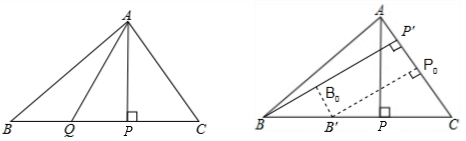
当点P在锐角△ABC最短边上的高的垂足的位置时,
PA+PB+PC最小.
证明:如图,P为△ABC一边BC边,
上的高的垂足,而Q为BC边上的任一点,
∵PA+PB+PC=PA+BC,QA+QB+QC=QA+BC,PA<QA,
∴PA+PB+PC<QA+QB+QC
又设AC为△ABC最短边,作这边上的高BP′(如图),
可知BP'>AP.
在BP′上截取BoP′=AP,在BC上截取B′C=AC,
作B′Po⊥AC.垂足为Po,
连接B′Bo.
∵Rt△APC≌Rt△B'PoC,
∴AP=B'Po=BoP'.
∵四边形B'BoP'Po是矩形,
∴∠B'BoB=90°,
在△B'BoB中,B'B>BBo,
∵P'A+P'B+P'C=BBo+AP+AC,PA+PB+PC=BP'+AC+AP,
∴P'A+P'B+P'C<PA+PB+PC.
