阅读下面现代文,完成问题。
到了盛夏三伏天,大伙都要把家里的物什抖出来在太阳底下晒一晒。冬袄夏衫,陈芝麻烂豆子,农家小院色彩斑斓起来。每当此时,必定爬着颤微微的木梯取下悬在屋梁上的书袋,忙着在院子里摆起陈书方阵。
梁上有多少书袋,可能只有父亲明白。随着姐姐和我相续步入学堂,书袋逐年增多。起初,书都是放在柜子里。每学期末,父亲总要花大约半天时间整理好我们姐妹俩用过的书籍,理得整整齐齐后放进柜子。一次暑假,父亲再次放书时发现柜子里的书残缺不全,拿出来仔细一看,原来家里的老鼠也要读书了,书页都被咬成锯齿状。自此,我们把书从地上转移到屋顶上。
还记得第一次上学领到新书回家后,父亲赶紧找来几张报纸教我包书皮。“新书,好好爱护,好好读。”父亲边说边极为小心地包好封皮,然后在封皮上一笔一划写下我的名字。父亲只上过4年学,后因无钱而退学。我不知道父亲为何如此爱书,但他在我幼小的心灵里植下的爱书种子却在悄悄发芽。从此,领到新书,我首先便是包书皮,不在书上乱画,更不会乱撕书页。
父亲常念叨的一句话是“万贯家财不如一卷香书”。农暇时,父亲常会拿起我们涂抹过的旧书饶有兴趣地读起来。尽管有的还是小学一年级的课本,可父亲乐在其中。
与父亲相比,母亲不仅对书,而且对一切有字的东西都怀虔诚之情。母亲没有踏入学堂一步,至今连自己的名字也不会写。母亲羡慕识字的人,更羡慕读书人。每当我和姐姐在灯下写作业时,夏天母亲会轻轻地摇着扇子驱赶蚊子,冬天母亲会默默烧一盆旺火驱走寒冷。
家里的每本书,乃至每张纸,母亲都会收拾好交给父亲整理。由于母亲不识字,凡遇到有字的纸片书本,也不知道有用与否,母亲全盘留下。曾经一次洗衣服,母亲忘了掏口袋,结果姐姐衣服口袋里的一张纸被浸湿揉乱。还记得放学回家,母亲忐忑不安地把一块一块粘贴在一起的纸片递给姐姐。也不知母亲东拼西凑粘贴了多久,可那纸片其实是一张草稿纸。每次母亲扫地,整理屋子,都会把飞扬的小纸片或是撕剩的半个本子小心翼翼地捡起来。无数次,我和姐姐大嚷那些是废纸,可是母亲微微一笑,“这些都是你们写过的东西,留着或许有用。”于是,凡是我们姐妹读过或写过的书本,全都被保存起来。
最难忘的是前年高考后的那天中午,父亲和母亲顶着骄阳赶到学校接我回家。
经过三天无硝烟的“战争”,我已筋疲力尽。宿舍里,父亲和母亲帮我收拾东西。被子、衣服塞进一个包里倒还省事,可堆积如山的书本、试卷却不好带走。父亲带来的麻袋已装满,可仍有好多书没有装下。
那些天,许多收购旧书的小贩已在宿舍前排起了长队。“挑些重要的书带回去,其余的卖了吧。”我提议道,那么多书拿起来很沉。“辛辛苦苦读的书,哪能不要呢!”母亲又继续往麻袋里塞,父亲则从小店里又弄来一个麻袋。从课本到试卷,从本子到草稿纸,母亲一点不剩地全装进麻袋里。
流火的七月,父亲弓着背,背着一麻袋书,母亲弓着背,背着一麻袋书。走出宿舍,小贩们立刻围上来。“不卖,不卖!”母亲极力从包围中往外挤。“什么?三毛钱一斤,你以为我背的是什么,这是书,这是宝!”父亲似乎有点愤怒,“你们买不起!”小贩们面面相觑,“第一次遇到这么奇怪的人。”一个小贩嘀咕道。
十几里路,三十几度高温,挥汗如雨赶到家时已直不起腰。他们脸上挂满汗珠,心里却乐开了花,因为我踏上异地求学的征途,更格外珍惜那些书。十几年的求学,几间小瓦房越来越破了,越来越空了,父母也越来越憔悴了,惟独梁上的书袋越来越多了。瓦房年久失修,每到春夏多雨时节,雨水顺着瓦缝流进屋里。高挂在梁上的书虽可逃鼠啃之苦,却免不了雨淋之灾。于是晒书成了父母伏天的头等大事。
爬上屋顶将积攒了几十年的书一捆一捆搬下来,而后又要一本一本扎好搬上去,对于年近五十的父母来说,这不是一件易事。可是每当矮小的瓦房前,简陋的篱笆院子里摆满大大小小的书本时,父亲会坐在一旁悠闲地吸着烟,“万贯家财不如一卷香书,我家可比百万富翁还富呀!”母亲则时不时翻动受潮的书,似乎在呵护一个宝贝。
又一个盛夏来临,故乡的小院里,父母又要为家里的“宝贝”忙碌了。(选自《青年文摘》2006年第一期,有删节)
1、文中对题目进行解说的一句话是:
_________________________________________________
2、文章写了父母爱书的几件事,请你用简洁的语言概括文中详写的一件事。
_________________________________________________
3、贯串全文的一条主线是什么?
_________________________________________________
4、试说说文章“照应”的运用。
_________________________________________________
5、从文中摘录一个细节描写的句子,并作点赏析。
_________________________________________________
6、文章流露出作者怎样的情感?
_________________________________________________
 倍.试求:
倍.试求:
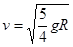 (2)
(2)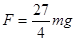 (3)
(3)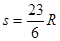
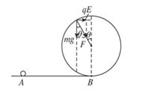
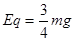
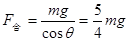 ……(1分)
……(1分) …………(2分)
…………(2分)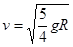 ……(1分)
……(1分)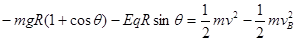 ………(2分)
………(2分)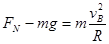 ………(1分) 解得:
………(1分) 解得: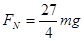 …(1分)
…(1分)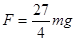 …(1分)
…(1分)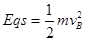 …(2分)
…(2分) ……(1分)
……(1分)