问题
计算题
如图，一小球A质量为m1=2kg在离桌面高为h1=0.04m处以初速度v0=3m/s沿一段粗糙的圆弧轨道下滑，圆弧轨道末端与桌面水平方向相切处有一质量为m2=1kg的小球B用一根长为L=0.08m的轻细绳静止悬挂着。两小球发生碰撞后，小球B恰好能绕细绳悬点O做圆周运动，小球A落在地面的水平距离为x=0.1m，已知桌子离地面高为h2=0.05m，不计空气阻力，重力加速度为g=10m/s2，求
（1）小球A碰后的速度为v1
（2）小球B碰后的速度为v2以及这时细绳对小球B的拉力FT
（3）小球A沿粗糙圆弧轨道下滑过程中，摩擦力所做的功Wf
答案
（1）1m/s (2)2m/s 60N (3)-5.8J
题目分析：（1）B球发生碰撞，在碰撞过程中可认为动量守恒，则
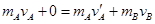
A球做平抛运动，则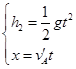
B球恰好能绕细绳悬点O做圆周运动，说明最高点速度为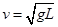
，根据机械能守恒定律则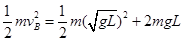
联立上式则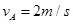
，
，
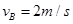
（2）根据向心力知识可得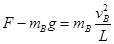
，则F=60N
（3）根据动能定理A下落到B处未碰撞之前，设速度为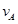
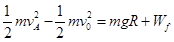
所以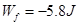
点评：本题考查了在碰撞过程中的动量守恒定律，并利用机械能守恒定律、动能定理列式求解，综合程度较高。