问题
计算题
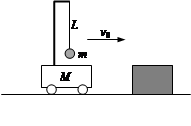
(原创)如图所示,小车连同其固定支架的总质量为M=3m,支架右端通过长为L的不可伸长的轻绳悬挂一质量为m的小球,轻绳可绕结点在竖直平面内转动,车和小球整体以速度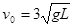 向右匀速行驶。突然,小车因撞到正前方固定障碍物,速度立即变为零,小球以v0为初速度开始在竖直平面内做圆周运动。当小球第一次到达最高点时,地面对车的支持力恰好为零。已知在此过程中,小车一直未动,重力加速度为g。求:
向右匀速行驶。突然,小车因撞到正前方固定障碍物,速度立即变为零,小球以v0为初速度开始在竖直平面内做圆周运动。当小球第一次到达最高点时,地面对车的支持力恰好为零。已知在此过程中,小车一直未动,重力加速度为g。求:
(1)小车与障碍物碰撞后瞬间,轻绳上的拉力大小;
(2)小球第一次到最高点时的速度大小;
(3)小球从最低点到第一次到达最高点过程中,克服空气阻力做的功。
答案
(1)10mg (2)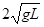 (3)
(3)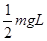
题目分析:(1)小车撞到障碍物瞬间,对小球
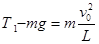 (3分)
(3分)
解得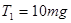 (1分)
(1分)
(2)小球过最高点时,对小车
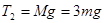 (3分)
(3分)
此时,对小球
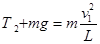 (3分)
(3分)
解得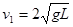 (1分)
(1分)
(3分)从小车与障碍物相撞到小球第一次运动到最高点,对小球
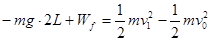 (4分)
(4分)
解得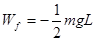 (1分)
(1分)
故,小球克服摩擦力做功为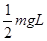 (1分)
(1分)
