问题
计算题
如下图所示的木板由倾斜部分和水平部分组成，两部分之间由一段圆弧面相连接．在木板的中间有位于竖直面内的光滑圆槽轨道，斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球，在施加于1号球的水平外力F的作用下均静止，力F与圆槽在同一竖直面内，此时1号球球心距它在水平槽运动时的球心高度差为h.现撤去力F使小球开始运动，直到所有小球均运动到水平槽内．重力加速度为g.求：
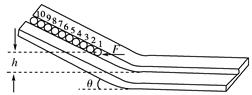
(1)水平外力F的大小；
(2)1号球刚运动到水平槽时的速度；
(3)整个运动过程中，2号球对1号球所做的功．
答案
(1)10mgtan θ (2)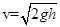 
(3)9mgrsin θ
题目分析：(1)以10个小球整体为研究对象，由力的平衡条件可得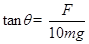
得F＝10mgtan θ.
(2)以1号球为研究对象，根据机械能守恒定律可得
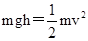解得
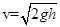
(3)撤去水平外力F后，以10个小球整体为研究对象，利用机械能守恒定律可得：
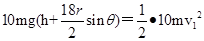解得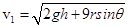
以1号球为研究对象，由动能定理得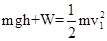
得W＝9mgrsin θ.
点评：本题解题关键有两个：一要选择研究对象，二是明确解题规律．当10个球都在斜面上下滑时，相互间没有作用力，机械能守恒．