问题
计算题
（1 0分）一种弹珠游戏如图，球1以初速v0出发，与球2发生弹性正碰，使球2进入洞中，但球1不能进洞。已知两球的质量比m1: m2=3:2，两球所受阻力均为自身重力的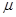
倍。开始时两球间距、球2与洞口间距均为L。求：
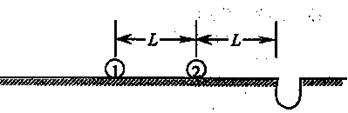
①两球碰撞完成的瞬间二者速度大小之比；
②为了能够完成任务，球1的初速度v0的最小值。
答案
①v1：v2=1:6 ②v0= 
题目分析：①两球碰撞过程满足动量守恒定律和机械能守恒定律，设碰前瞬间球1的速度为v
m1v=m1v1+m2v2
m1v2/2=m1v12/2+m2v22/2
可得：v1=v/5,v2=6v/5
两者速度之比v1：v2=1:6
②当球1初速度最小时，碰后小球2应刚好落入洞中有
µm2gL=m2v22/2
碰前球1做减速运动
-µm1gL=m1v2/2- m1v02/2
可得 v0=