问题
计算题
为满足不同列车间车厢进行重新组合的需要，通常需要将相关的列车通过“驼峰”送入编组场后进行重组（如图所示），重组后的车厢同一组的分布在同一轨道上，但需要挂接在一起。现有一列火车共有 n节车厢，需要在编好组的“驼峰”左侧逐一撞接在一起。已知各车厢之间间隙均为s0，每节车厢的质量都相等，现有质量与车厢质量相等、且没有动力驱动的机车经过“驼峰”以速度v0向第一节车厢运动，碰撞后通过“詹天佑挂钩”连接在一起，再共同去撞击第二节车厢，直到 n 节全部挂好。不计车厢在挂接中所受到的阻力及碰撞过程所需的时间，求：
（1）这列火车的挂接结束时速度的大小；
（2）机车带动第一节车厢完成整个撞接过程所经历的时间。
（3）这列火车完成所有车厢挂接后，机车立即开启动力驱动，功率恒为P，在行驶中的阻力f恒定，经历时间t达到最大速度，求机车此过程的位移。
答案
：（1）vn= v0/（n+1）
（2）t总= t1+t2+t3+……+ tn-1=s0[2+3+4+……+n]/v0=
（３）
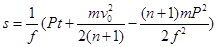
题目分析：（1）用v′表示整列车厢最后的速度，用m表示每节车厢的质量，由于轨道对车厢的阻力不计，所以由n节车厢组成的系统，动量守恒，即：mv=（n+1）mv′，得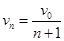
（2）设机车带动第一节车厢与第2、…、n-1次碰撞后连在一起的车厢速度分别为v2、v3、…、vn，则有：
mv0=2mv1
mv0=3mv2
…….
mv0=nmvn-1
所以整个挂接过程所用时间为：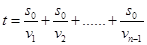
=
=
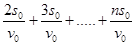(2)列车所能达到的最大速度为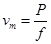
，
根据动能定理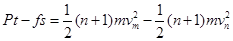 
，
解得：