问题
计算题
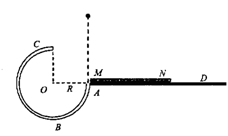
(18分）如图所示，一个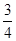
圆弧形光滑细圆管轨道ABC，放置在竖直平面内．轨道半径为R，在A点与水半地面AD相接，地面与圆心O等高，MN是放在水平地面上长为3R，厚度不计的垫子，左端M正好位于A点将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放，不考虑空气阻力。
（1）若小球从C点射出后恰好能打到垫子的M端，则小球经过C点时对管的作用力大小和方向如何？
（2）欲使小球能通过C点落到垫子上，小球离A点的高度H应是多少？
答案
（1）小球对管子作用力大小为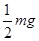
，方向竖直向下
（2）H的高度应为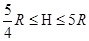 
题目分析：（1）小球离开C点做平抛运动，落到M点时水平位移为R，竖直下落高度为R，根据平抛运动规律可得：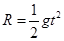
（1分）
运动时间
（1分）
从C点射出的速度为
（2分）
设小球以v1经过C点受到管子对它的作用力为N，由向心力公式可得
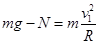（2分）
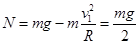， （1分）
由牛顿第三定律知，小球对管子作用力大小为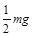
，方向竖直向下． （1分）
（2）小球落到M点时，对应小球下降的最小高度为H1 ，根据机械能守恒定律可得
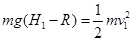（2分）
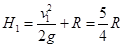（1分）
小球下降的高度最高时，小球运动的水平位移为4R，打到N点．
设能够落到N点的水平速度为v2，根据平抛运动规律可得：
（2分）
设小球下降的最大高度为H2 ，根据机械能守恒定律可得
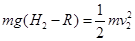（2分）
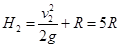（1分）
故H的高度应为 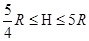（2分）