阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。
【说明】某工程计算中要完成多个矩阵相乘(链乘)的计算任务。
两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法,计算,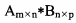 需要m*n*p次乘法运算。
需要m*n*p次乘法运算。
矩阵相乘满足结合律,多个矩阵相乘,不同的计算顺序会产生不同的计算量。以矩阵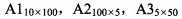 三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行10*100*5+10*5*50=7500次乘法运算;若按A1*(A2*A3)计算,则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。矩阵链乘问题可描述为:给定n个矩阵,矩阵Ai的维数为
三个矩阵相乘为例,若按(A1*A2)*A3计算,则需要进行10*100*5+10*5*50=7500次乘法运算;若按A1*(A2*A3)计算,则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。矩阵链乘问题可描述为:给定n个矩阵,矩阵Ai的维数为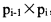 ,其中i=1,2,…,n。确定一种乘法顺序,使得这n个矩阵相乘时进行乘法的运算次数最少。
,其中i=1,2,…,n。确定一种乘法顺序,使得这n个矩阵相乘时进行乘法的运算次数最少。
由于可能的计算顺序数量非常庞大,对较大的n,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵链乘问题具有最优子结构,即若A1*A2*…*An的一个最优计算顺序从第k个矩阵处断开,即分为A1*A2*…*Ak和Ak+1*Ak+2*…*An两个子问题,则该最优解应该包含A1*A2*…*Ak的一个最优计算顺序和Ak+1*Ak+2*…*An的一个最优计算顺序。据此构造递归式,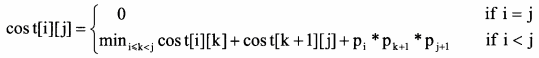
其中,cost[i][j]表示Ai+1*Ai+2*…*Aj+1的最优计算的计算代价。最终需要求解cost[0][n-1]。
【C代码】算法实现采用自底向上的计算过程。首先计算两个矩阵相乘的计算量,然后依次计算3个矩阵、4个矩阵"""n个矩阵相乘的最小计算量及最优计算顺序。下面是该算法的C语言实现。(1)主要变量说明n:矩阵数seq[]:矩阵维数序列cost[][]:二维数组,长度为n*n,其中元素cost[i][j]表示Ai+1*Ai+2*…*Aj+1的最优计算的计算代价trace[][]:二维数组,长度为n*n,其中元素trace[i][j]表示Ai+1*Ai+2*…*Aj+1的最优计算对应的划分位置,即k(2)函数cmm
问题1:根据以上说明和C代码,填充C代码中的空(1)~(4)。 问题2:根据以上说明和C代码,该问题采用了(5)算法设计策略,时间复杂度为(6)(用O符号表示)。 问题3:考虑实例n-6,各个矩阵的维数:A1为5*10,A2为10*3,A3为3*12,A4为12*5,A5为5*50,A6为50*6,即维数序列为5,10,3,12,5,50,6。则根据上述C代码得到的一个最优计算顺序为(7)(用加括号方式表示计算顺序),所需要的乘法运算次数为(8)。
参考答案:
问题1:(1)i)
问题2:O(n3)
问题3:(7)((A1A2)((A3A4)(A5A6)))(8)2010
解析:
本题考查算法设计、分析和C程序实现的应用知识,属于传统题目,考查点也与往年类似。题干部分较清楚的描述了求解矩阵链乘问题的算法,理解递归式是关键,n个矩阵相乘是一个规模为n的问题,从某个k处断开,该问题可以分解为两个子问题,即A1*A2*…*An分为A1*A2*…*Ak和Ak+1*Ak+2*…*An两个子问题。求解时采用自底向上的方法。
【问题1】本问题考查算法的实现。C程序中主要部分是三重循环,循环变量p定义了求解问题的规模,因为是自底向上,因此,p的值应该是从1到n-1,即从规模为1的问题一直到规模为n-1的问题。循环变量i是要求解的子问题的起始,从0开始,最大为n-p-1,故(1)处应填n-p。确定了i和p之后,下来就要确定j了,显然,空(2)处为j=i+p。循环变量k是问题Ai*Ai+1*…*Aj的划分位置,对每一个k,都要计算需要的计算成本,可以根据递归式来填写,空(3)处为cost[i][k]+cost[k+1][j]+seq[i]*seq[k+1]*seq[j+1]。确定每个问题Ai*Ai+1*…*Aj的划分位置k之后,要把这个k值记住,放在变量tempTrace中,即空(4)处填写tempTrace=k。
【问题2】本问题考查算法的设计策略和时间复杂度,从题干说明可以很容易看出,问题具有最优子结构和重叠子问题,采用自底向上的方法求解,这些都是动态规划的典型特点,因此采用的是动态规划设计策略。从上述C程序很容易分析出,程序中没有递归,存在三重循环,故时间复杂度为O(n)。
【问题3】本问题考查算法的应用。通过一个具体实例可以更容易理解问题和求解方法。可以根据问题1中的程序执行来求解。启发式的思路是先把维度最大的消掉,如A5*A6相乘之后,维度50就没有了,所以考虑这两个矩阵先相乘;然后是A3*A4相乘之后,维度12就没有了,所以考虑这两个矩阵相乘;接着,A1*A2相乘之后,维度10就没有了,所以考虑这两个矩阵相乘……这样可以确定相乘的顺序((A1A2)((A3A4)(A5A6))),需要的计算开销分别是5*50*6=1500,3*12*5=180,5*10*3=150,3*5*6=90,5*3*6=90,把上述值相加,即1500+180+150+90+90=2010。

 片的含量时,在308nm处测得供试品溶液的吸收度为0.638,已知氯氮
片的含量时,在308nm处测得供试品溶液的吸收度为0.638,已知氯氮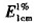 )为319,则供试品溶液的浓度为()
)为319,则供试品溶液的浓度为()