问题
计算题
（10分） 如图所示，一带电平行板电容器水平放置，金属板M上开有一小孔．有A、B、C三个质量均为m、电荷量均为＋q的带电小球（可视为质点），其间用长为L的绝缘轻杆相连，处于竖直状态．已知M、N两板间距为3L，现使A小球恰好位于小孔中，由静止释放并让三个带电小球保持竖直下落，当A球到达N极板时速度刚好为零，求：
⑴三个小球从静止开始运动到A球刚好到达N板的过程中，重力势能的减少量；
⑵两极板间的电压；
⑶小球在运动过程中的最大速率．
答案
⑴ 9mgL ⑵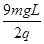 
⑶ 
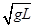
题目分析：⑴设三个球重力势能减少量为△Ep
△Ep= 9mgL 2分
⑵设两极板电压为U ，由动能定理：W合＝△Ek
有3mg·3L－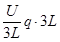
－
－
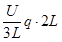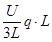＝0
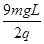解得：U = 4分
⑶当小球受到的重力与电场力相等时，小球的速度最大vm
3mg=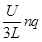
解得 n=2
即：小球达到最大速度的位置是B球刚进入电场时的位置，由动能定理有：
3mg·L-=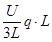 
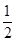×3mvm2
解得vm=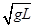 4分