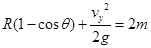问题
计算题
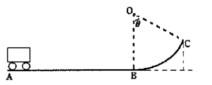
(12分)如图长为L=1.5m的水平轨道AB和光滑圆弧轨道BC平滑相接,圆弧轨道半径R=3m,圆心在B点正上方O处,弧BC所对的圆心角为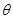 =53O,具有动力装置的玩具小车质量为m=1kg,从A点开始以恒定功率P=10w由静止开始启动,运动至B点时撤去动力,小车继续沿圆弧轨道运动并冲出轨道。已知小车运动到B点时轨道对小车的支持力为FB=26
=53O,具有动力装置的玩具小车质量为m=1kg,从A点开始以恒定功率P=10w由静止开始启动,运动至B点时撤去动力,小车继续沿圆弧轨道运动并冲出轨道。已知小车运动到B点时轨道对小车的支持力为FB=26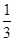 N,小车在轨道AB上运动过程所受阻力大小恒为f=0.1mg小车可以被看成质点。取g=10m/s2,,sin53o=0.8,cos53o=0.6,求:
N,小车在轨道AB上运动过程所受阻力大小恒为f=0.1mg小车可以被看成质点。取g=10m/s2,,sin53o=0.8,cos53o=0.6,求:
(1)动力小车运动至B点时的速度VB的大小;
(2)小车加速运动的时间t;
(3)小车从BC弧形轨道冲出后能达到的最大离地高度。
答案
(1)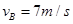 (2)
(2)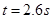 (3)
(3)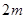
题目分析:(1)B点为圆周运动最低点,重力支持力的合力提供向心力,即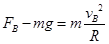
带入数据得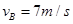
(2)小车以恒定功率P=10w由静止开始启动,经过B点时的牵引力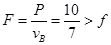 ,所以从A到B小车一直在加速,根据动能定理有
,所以从A到B小车一直在加速,根据动能定理有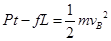
整理得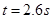
(3)小车从B点到C点的过程,根据动能定理有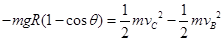
离开轨道后,水平方向为匀速直线运动,初速度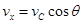
竖直方向匀减速直线运动,初速度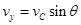 ,速度减小到0时上升到最高点,即
,速度减小到0时上升到最高点,即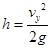
小车从BC弧形轨道冲出后能达到的最大离地高度为