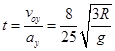问题
计算题
（16分）如图所示，矩形区域MNPQ内有水平向右的匀强电场；在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小为B。半径为R的光滑绝缘空心半圆细管ADO固定在竖直平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN。一质量为m、电荷量为q的带正电小球（可视为质点）从半圆管的A点由静止滑入管内，从O点穿出后恰好通过O点正下方的C点。已知重力加速度为g，电场强度的大小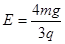
。求：
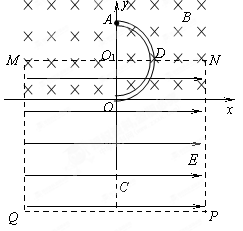
⑴小球到达O点时，半圆管对它作用力的大小；
⑵矩形区域MNPQ的高度H和宽度L应满足的条件；
⑶从O点开始计时，经过多长时间小球的动能最小？
答案
（1）
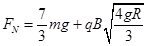（2）
，
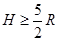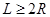（3）
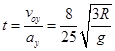
题目分析：⑴从A→O过程，由动能定理得：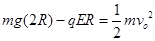
（2分）
解得：
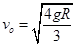（1分）
在O点，由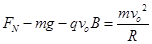
（2分）
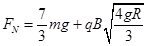得 （1分）
(2)小球从O→C 过程： 水平方向做匀减速运动，竖直方向做自由落体运动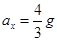
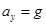
设向左减速时间为t，则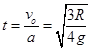
（1分）
水平位移大小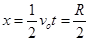
（1分）
竖直位移大小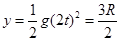
（1分）
高度满足条件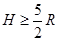（1分）
宽度应满足条件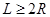（1分）
（3）以合力F方向、垂直于合力方向分别建立x-y坐标系，并将速度分别沿x、y方向分解，如图所示；当F与速度v垂直时，小球的速度最小，动能最小，设经过的时间为t，
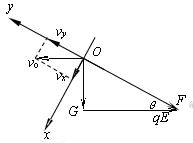
由几何关系知：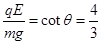
在y方向：初速度为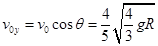
；末速度为零；加速度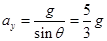
所以运动的时间