（20分）如图，光滑绝缘 * * 台距水平地面高H=0.80m,地面与竖直绝缘光滑圆形轨道在A点连接,A点距竖直墙壁s=0.60m,整个装置位于水平向右的匀强电场中。现将一质量m=0.1kg，电荷量q=10-3C的正电荷小球（可视为质点）从平台上端点N由静止释放,离开平台N后，恰好切入半径为R=0.4m的绝缘光滑圆形轨道，并沿轨道运动到P点射出。图中O点是圆轨道的圆心，BC分别是原先轨道的最低和最高点，AO、BO间夹角为53°。(取g=10m/s2,sin53°=0.8,cos53°=0.6)求：
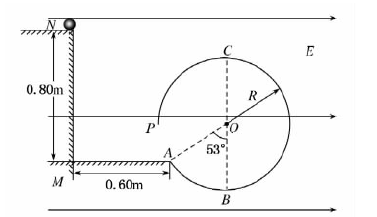
（１）电场强度E的大小；
（２）小球到A点的速度大小和方向；
（３）小球对轨道最大压力。
（1）
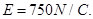（2）速度方向与水平方向成
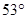.大小为5m/s（3）10N
题目分析：（1) 小球离开N点后
竖直方向只有重力作用，初速度0，所以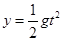
(1分)
水平方向只受到电场力作用，初速度0，所以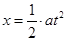 
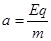； (1分)
(1分)
几何关系如下图
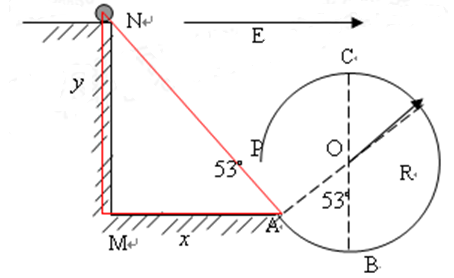
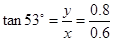(2分)
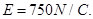代入数据可得 (1分)
（2)
由公式v2="2ax" 可得
竖直方向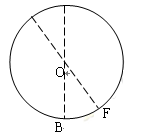
水平方向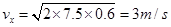
根据速度的矢量合成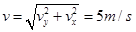
(4分)
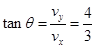，速度方向与水平方向成 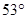(2分)
（3）电场力和重力的合力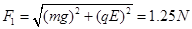
，假设合力与竖直方向夹角
，
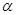则有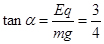
，所以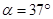
，方向沿OF方向。
合力大小方向均不变，可等效为重力，所以等效重力为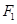
。F点即为等效重力的最低点
最大速度在如图所示的F点，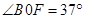
从N点到F点由动能定理可知
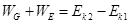
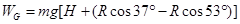
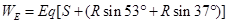
代入数据可得F点的速度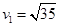
m/s (3分)
在F点：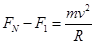
(2分)
代入数据可得
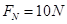(1分)
根据牛顿第三定律：小球对轨道最大压力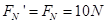
( 2分)