问题
计算题
（16分）如图所示，倾角为θ的固定斜面的底端有一挡板M，轻弹簧的下端固定在挡板M上，在自然长度下，弹簧的上端在O位置。质量为m的物块A（可视为质点）从P点以初速度v0沿斜面向下运动，PO＝x0，物块A与弹簧接触后将弹簧上端压到O＇点位置，然后A被弹簧弹回。A离开弹簧后，恰好能回到P点。已知A与斜面间的动摩擦因数为μ，重力加速度用g表示。求：
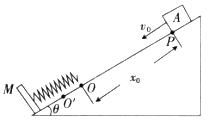
（1）物块A运动到O点的速度大小；
（2）O点和O＇点间的距离x1；
（3）在压缩过程中弹簧具有的最大弹性势能EP。
答案
（1）
（2）
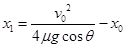（3）
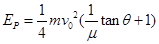
题目分析：（1）A从P点运动到O点，只有重力和摩擦力做功，由动能定理可知：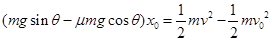
（3分）
得：（2分）
（2）A从P点向下运动再向上运动回到P点的全过程中，根据动能定理：
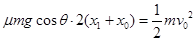（3分）
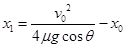（2分）
（3）A从O′点向上运动到P点的过程中，由能量守恒定律可知：
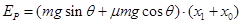（3分）
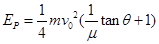解得 （3分）
