阅读下列说明和C代码，回答问题1至问题3，将解答写在答题纸的对应栏内。
【说明】计算一个整数数组a的最长递增子序列长度的方法描述如下：假设数组a的长度为n，用数组b的元素b［i］记录以a［i］（0≤i≤n）为结尾元素的最长递增子序列的长度，则数组a的最长递增子序列的长度为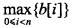
；其中b［i］满足最优子结构，可递归定义为：
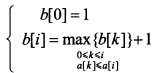【C代码】下面是算法的C语言实现。（1）常量和变量说明a：长度为n的整数数组，待求其最长递增子序列b：长度为n的数组，b［i］记录以a［i］（0≤i≤n）为结尾元素的最长递增子序列的长度，其中0≤i
问题1：根据说明和C代码，填充C代码中的空（1）～（4）。 问题2：根据说明和C代码，算法采用了（5）设计策略，时间复杂度为（6）（用O符号表示）。 问题3：已知数组a={3，10，5，15，6，8}，根据说明和C代码，给出数组b的元素值。
参考答案：
问题1：（1）b［0］=1（2）j）
问题2：O（n 2）
问题3：b={1，2，2，3，3，4}
解析：
本题考查算法设计与分析以及用C程序设计语言来实现算法的能力。此类题目要求考生认真阅读题目对问题的描述，理解算法思想，并会用C程序设计语言来实现。
【问题1】根据题干描述，用一个数组b来记录数组a每个子数组的最长递增子序列的长度，即b［i］记录a［0..i］的最长递增子序列的长度。首先，只有一个元素的数组的最长递增子序列的长度为1，即给b［0］直接赋值1。因此，空（1）处填写"b［0］=1"。两重for循环中，第一重是从a数组的第二个元素开始，考虑每个子数组a［0..i］的最长递增子序列的长度，第二重是具体的计算过程。考虑子数组a［0..i］，其最长递增子序列的长度应该等于子数组a［0..i-1］中的比元素a［i］小的元素的最长递增子序列的长度加1，当然，可能存在多个元素比元素a［i］小，那么存在多个最长递增子序列的长度，此时，取最大者。因此，空处填写"j来实现的。另外，计算的过程不是采用递归的方式，而是以一种自底向上的方式进行的。
【问题2】从题干说明和C程序来看，这是一个最优化问题，而且问题具有最优子结构，一个序列的最长递增子序列由其子序列的最长递增子序列构成。在计算过程中采用了自底向上的方式来进行，这具有典型的动态规划特征。因此采用的是动态规划设计策略。C程序中，有两重for循环，因此时间复杂度为O（n）。
【问题3】输入数组为数组a={3，10，5，15，6，8}，很容易得到，子数组a［0..0］，a［0..1］，…，a［0..5］的最长递增子序列的长度分别为1，2，2，3，3，4，因此答案为b={1，2，2，3，3，4}。该题可以根据题干说明、C代码来计算。由于输入很简单，答案也可以从输入直接计算出来。