问题
选择题
一摩托车在竖直的圆轨道内侧做匀速圆周运动，周期为T，人和车的总质量为m，轨道半径为R，车经最高点时发动机功率为P0，车对轨道的压力为2mg。设轨道对摩托车的阻力与车对轨道的压力成正比，则（ ）
A．车经最低点时对轨道的压力为4mg
B．车经最低点时发动机功率为2P0
C．车从最高点经半周到最低点的过程中发动机做的功为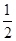
P0T
D．车从最低点经半周到最高点的过程中发动机做的功为2mgR
答案
AB
题目分析:在最高点：向心力大小为 Fn=N1+mg=3mg，摩托车做匀速圆周运动，向心力大小不变，则
在最低点：Fn =N2-mg，得N2=4mg．故A正确；在最高点：发动机功率P0=F1v=μN1v=2μmgv，在最低点：发动机功率P=F2v=μN2v=4μmgv，则P=2P0．故B正确；由上分析可知，车从最高点经半周到最低点的过程中发动机的平均功率大于P0，发动机做的功大于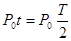
．故C错误；摩托车做匀速圆周运动，动能不变，根据动能定理，得知其合力做功为零，则发动机做功等于重力做功与摩擦力做功之和，发动机做的功不等于2mgR．故D错误。