阅读下列说明、图和C代码，将应填入（n）处的字句写在答题纸的对应栏内。
说明：一般的树结构常采用孩子一兄弟表示法表示，即用二叉链表作树的存储结构，链表中节点的两个链域分别指向该节点的第一个孩子节点和下一个兄弟节点。例如，题图4-1（a）所示的树的孩子一兄弟表示如题图4-1（b）所示。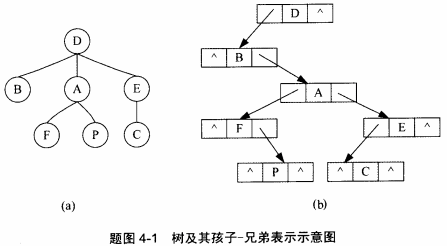
函数LevelTraverse（）的功能是对给定树进行层序遍历。例如，对题图4-1所示的树进行层序遍历时，节点的访问次序为：DBAEFPC。
对树进行层序遍历时使用了队列结构，实现队列基本操作的函数原型如下表所示。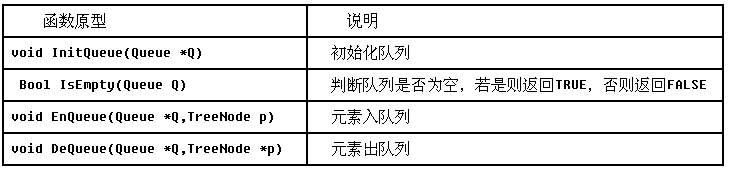
Bool、Status类型定义如下：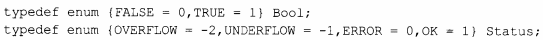
树的二叉链表节点定义如下：
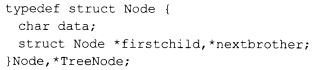
函数如下：
参考答案：
（1）EnQueue（&tempQ，root）
（2）brotherptFbrotherptr>nextbrother
（3）!IsEmpty（tempQ）
（4）DeQueue（&tempQ，&ptr）
（5）!ptr->firstchild
（6）EnQueue（&tempQ，ptr->firstchilD.
（7）brotherptr=brotherptr->nextbrother
解析：
解答此题的关键在于理解用队列层序遍历树的过程。算法的流程是这样的：首先将树根节点入队，然后将其所有兄弟节点入队（当然，由于是根节点，故无兄弟节点）；完成这一操作以后，便开始出队、打印；在打印完了之后，需要进行一个判断，判断当前节点有无孩子节点，若有孩子节点，则将孩子节点入队，同时将孩子节点的所有兄弟节点入队；完了以后继续进行出队操作，出队后再次判断当前节点是否有孩子节点，并重复上述过程，直至所有节点输出。接下来以本题为例来说明此过程。首先将树根节点D入队，并同时检查是否有兄弟节点，对于兄弟节点则一并入队。这里的D没有兄弟节点，所以队列此时应是：D。接下来执行出队操作。D出队，出队以后检查D是否有子节点，经检查，D有子节点B，所以将B入队，同时将B的兄弟节点A和E按顺序入队。得到队列：B、A、E。接下来再执行出队操作。B出队，同时检查B是否有子节点，B无子节点，所以继续执行出队操作。A出队，同时检查A是否有子节点，A有子节点F，所以将F入队，同时将F的兄弟节点P入队。得到队列：E、F、P。接下来再次执行出队操作。E出队，E有子节点C，所以C入队。得到队列：F、P、C。接下来再次执行出队操作。F出队，F无子节点，继续出队操作，P出队，P仍无子节点，最后C出队，整个过程结束。通过对算法的详细分析，可以轻松得到答案。
空（1）处应是对根节点root执行入队操作，即EnQueue（&tempQ，root）。
空（2）处在一个循环当中，循环变量是brotherptr，此变量无语句对其进行更新，所以空（2）处必定是更新brotherptr。结合前面的算法分析可知空（2）处应填入brotherptr=brotherptr->nextbrother。
空（3）处和空（4）处加上后面的语句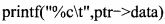
是控制数据的输出，这些数据应是从队列中得到，所以此处必有出队操作，同时在出队之前应判断队列是否为空，所以空（3）处和空（4）处应填入!IsEmpty（tempQ）和DeQueue（&tempQ，＆ptr）。
空（5）处实际上是问："在什么情况下，要持续进行出队操作？"前面的算法分析中已指出：若出队节点无子节点，则继续进行出队操作，所以空（5）处应填入!ptr->firstchild。空（6）处和空（7）处所在的语句段的功能是将刚出队节点的子节点及其兄弟节点入队，所以空（6）处应填入EnQueue（&tempQ，ptr->firstchild）。空（7）处和空（2）处相同，应填入brotherptr=brotherptr->nextbrother.