问题
计算题
（18分）一圆筒的横截面如图所示，其圆心为O。筒内有垂直于纸面向里的匀强磁场，磁感应强度为B。圆筒下面有相距为d的平行金属板M、N，其中M板带正电荷，N板带等量负电荷。质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放，经N板的小孔S以速度v沿半径SO方向射入磁场中，粒子与圈筒发生两次碰撞后仍从S孔射出，设粒子与圆筒碰撞过程中没有动能损失，且电荷量保持不变，在不计重力的情况下，求：
（1）M、N间电场强度E的大小；
（2）圆筒的半径R；
（3）保持M、N间电场强度E不变，仅将M板向上平移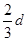
，粒子仍从M板边缘的P处由静止释放粒子自进入圆筒至从S孔射出期间，与圆筒的碰撞次数n。
答案
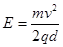
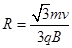n=3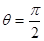
题目分析： (1)设两极板间的电压为U，由动能定理得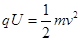 
由匀强电场中电势差与电场强度的关系得 U="Ed"
联立上式可得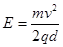
(2)粒子进入磁场后做匀速圆周运动，运用几何关系做出圆心O’， 圆半径为r，设第一次碰撞点为A，由于粒子与圆筒发生两次碰撞又从S孔射出，因此SA弧所对圆心角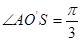
由几何关系得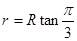 
粒子运动过程中洛伦兹力充当向心力，由牛顿第二定律，得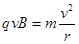 
联立得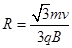
(3)保持M、N间电场强度E不变，M板向上平移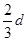
后，设板间电压为
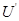，则
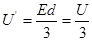
设粒子进入S孔时的速度为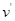
，由
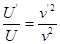可得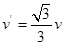
设粒子做圆周运动的半径为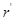
， 
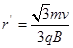
设粒子从S到第一次与圆筒碰撞期间的轨道所对圆心角为
，比较两式得到
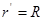，可见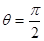
粒子须经过这样的圆弧才能从S孔射出，故 n=3