问题
解答题
两个全等的三角形ABC和DEF重叠在一起,△ABC的面积为3,且AB=CB,固定△ABC不动,将△DEF进行如下操作:
(1)如图(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积;
(2)如图(2),当D点向右平移到B点时,试判断CE与BF的位置关系,并说明理由;
(3)在(2)的条件下,若∠AEC=15°,求AB的长。
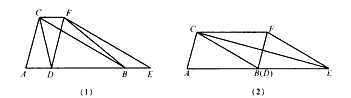
答案
解:(1)设△ABC的高为h,由题意,知CF=AD,
∴S梯形CDBF=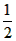 (AD+DB)h=
(AD+DB)h=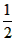 AB·h=S△ABC=3;
AB·h=S△ABC=3;
(2)由题意知CF∥BE且CF=BE,
∴四边形CBEF为平行四边形,
又∵BC=BE,
∴□CBEF为菱形,
∴CE⊥ BF;
(3)∵BC= BE,
∴∠ABC=2∠AEC=30°,
如图,作CG⊥AB于G,则CG=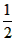 BC=
BC=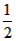 AB,
AB,
由S△ABC=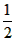 CG·AB=
CG·AB=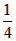 AB2=3,
AB2=3,
解得AB=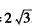 。
。
单项选择题
