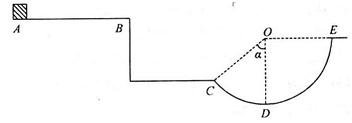
如图所示,质量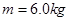 的滑块(可视为质点),在F=60N的水平拉力作用下从A点由静止开始运动,一段时间后撤去拉力F,当滑块由平台边缘B点飞出后,恰能从水平地面上的C点沿切线方向落入竖直圆弧轨道CDE,并从轨道边缘E点竖直向上飞出,经过0.4 s后落回E点。已知AB间的距离L="2.3" m,滑块与平台间的动摩擦因数
的滑块(可视为质点),在F=60N的水平拉力作用下从A点由静止开始运动,一段时间后撤去拉力F,当滑块由平台边缘B点飞出后,恰能从水平地面上的C点沿切线方向落入竖直圆弧轨道CDE,并从轨道边缘E点竖直向上飞出,经过0.4 s后落回E点。已知AB间的距离L="2.3" m,滑块与平台间的动摩擦因数 ,平台离地高度
,平台离地高度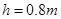 ,B、C两点间水平距离s="1.2" m,圆弧轨道半径R=1.0m。重力加速度g取10 m/s2,不计空气阻力。求:
,B、C两点间水平距离s="1.2" m,圆弧轨道半径R=1.0m。重力加速度g取10 m/s2,不计空气阻力。求:
(1)滑块运动到B点时的速度大小;
(2)滑块在平台上运动时受水平拉力F作用的时间;
(3)分析滑块能否再次经过C点。
(1)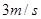 (2)
(2)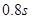 (3)能
(3)能
题目分析:(1)滑块由B至C的过程中做平抛运动
水平方向: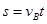 1分
1分
竖直方向: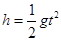 1分
1分
解得: 1分
1分
(2)滑块由A至B的过程中,F作用时间内做匀加速直线运动
 1分
1分
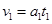 1分
1分
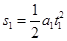 1分
1分
撤去F后滑块做匀减速直线运动
 1分
1分
 1分
1分
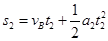 1分
1分
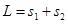 1分
1分
联立得: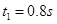 1分
1分
(3)由B至C的过程根据动能定理
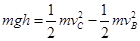 2分
2分
得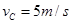
因此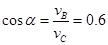 1分
1分
滑块从E点上抛至落回的时间用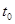 表示,则
表示,则
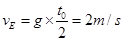 1分
1分
滑块沿圆弧轨道由C到E过程,设克服摩擦力做的功为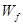
根据动能定理: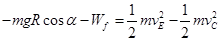 2分
2分
可得: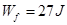
由E点返回到C点过程,
由于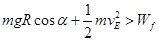
又因为返回过程中,克服摩擦力做功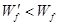 ,故滑决一定能再次经过C点 2分
,故滑决一定能再次经过C点 2分
