利用如图1所示装置探究动能定理,在斜面体的斜面上,一质量为1kg的物块后面固定一条通过打点计时器的纸带.先打点,然后让物块从静止开始沿斜面匀加速下滑,得到一条如图2所示的纸带.O点为打点的第一个点,A、B、C、D、E、F、H是计数点,每相邻两计数点间还有4个点没有标出,OA=17.65cm、AB=11.81cm、BC=14.79cm、CD=17.80cm、DE=20.81cm、EF=23.80cm、FH=26.79cm,根据以上数据进行下列处理.(g=10m/s2)
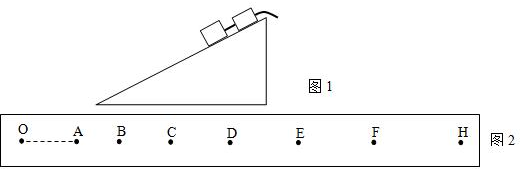
(1)物块匀加速下滑的加速度是______m/s2,物体所受的合外力是______N(结果保留三位有效数字).
(2)完成表格
| 从0点到各点的过程 合力所做的功W 单位(J) | 各点的动能EK 单位(J) | ||
| OB | 0.8838 | B | 0.8845 |
| OC | 1.3275 | C | 1.3276 |
| OD | ______ | D | 1.8634 |
| OE | 2.4858 | E | ______ |
| OF | 3.1998 | F | 3.1992 |

(4)根据(2)表中的数据和(3)中的图线,实验结论是______.
(1)由图可知,OA段不准确,故应从A点开始计算;因每两点之间还有4个点,故两计数点间的时间间隔为T=5×0.02s=0.1s;则由逐差法可得:
a=
=DH-AD 9T2
m/s2=3.00m/s2;(26.79+23.80+20.81)-(11.81+14.79+17.80) 9×0.01
由F=ma得,F=1×3.00m/s2=3.00N;
(2)OD段的位移L=(17.65+11.81+14.79+17.80)cm=62.05cm;
合外力的功W=FL=3.00×0.6305m=1.8615J;
E点的速度v=
=DF 2×0.1
m/s=2.2305m/s; 20.81+23.80 0.2
E点的动能E=
mv2≈2.4876J;1 2
(3)如图建立直角坐标系,将动能和功作为坐标轴,通过描点法得出图象如图所示:
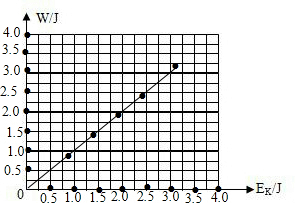
(4)由图象分析可知,在误差允许的范围内,合外力做的功等于物体动能的增加量;
故答案为:(1)3.00;3.00; (2)2.2305; 2.4876; (3)如上图所示;(4)在误差允许的范围内,合外力的功等于物体动能的增加量.
