问题
解答题
如图（Ⅰ），在平面直角坐标系中，⊙O′是以点O′（2，-2）为圆心，半径为2的圆，⊙O′′是以点O″（0，4）为圆心，半径为2的圆。
（1）将⊙O′竖直向上平移2个单位，得到⊙O1，将⊙O″水平向左平移1个单位，得到⊙O2如图（Ⅱ），分别求出⊙O1和⊙O2的圆心坐标；
（2）两圆平移后，⊙O2与y轴交于A、B两点，过A、B两点分别作⊙O2的切线，交x轴与C、D两点，求△O2AC和△O2BD的面积。
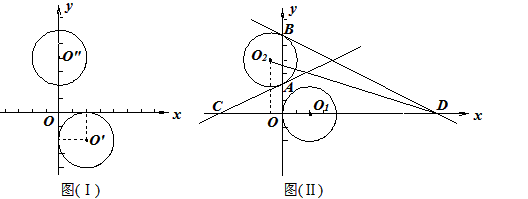
答案
解：（1）∵-2+2=0，
∴点O1的坐标为：（2，0），
∵0-1=-1，
∴点O2的坐标为：（-1，4）；
（2）如图，连接O2A，O2B，
∵⊙O2的半径为2，圆心O2到y轴的距离是1，
∴∠O2AB=∠O2BA=30°，
∴AB=2×2cos30°=2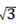
，
∴点A、B的坐标分别为A（0，4-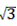
），B（0，4+），
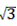∵AC，BD都是⊙O2的切线，
∴∠OAC=180°-90°-30°=60°，∠OBD=90°-30°=60°，
∴AC=（4-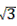
）÷cos60°=8-2
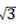，BD=（4+
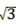）÷cos60°=8+2
，
∴
=
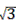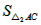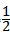×AC×O2A=
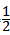×（8-2
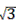）×2=8-2
，
=
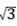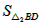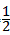×BD×O2B=
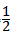×（8+2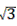
）×2=8+2
，
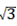故答案为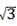：8-2
，8+2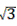
。
