问题
问答题
①某同学探究恒力做功和物体动能变化间的关系,方案如图所示.他想用钩码的重力表示小车受到的合外力,为减小这种做法带来的误差,实验中要采取的两项措施是:
a______b______
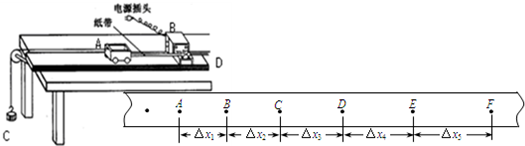
②如图所示是某次实验中得到的一条纸带,其中A、B、C、D、E、F是计数点,相邻计数点间的时间间隔为T.距离如图.则打B点时的速度为______;要验证合外力的功与动能变化间的关系,测得位移和速度后,还要测出的物理量有______
答案
①小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;
设绳子上拉力为F,对小车根据牛顿第二定律有:
F=Ma ①
钩码有:mg-F=ma ②
F=
=mgM M+m
,由此可知当M>>m时,够码的重力等于绳子的拉力即为小车是合外力.mg 1+ m M
故答案为:①a 平衡摩擦力; b 钩码的重力远小于小车的总重力(钩码的质量远远小于小车的质量).
②根据在匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小可知B点的速度大小为:
vB=(△x1+△x2) 2T
验证合外力的功与动能变化间的关系的原理:mgx=
Mv2,由此可知需要测量的物理量有:钩码质量m,小车的质量M,位移x,速度v. 1 2
故答案为:vB=
;钩码的质量m,小车的质量M.(△x1+△x2) 2T
