如图所示,均匀光滑直杆AB长为L,可绕光滑固定转轴O转动,O在距B点处.在水平杆的另一端A下摆经过的轨迹上安装光电门,用来测量A端的瞬时速度vA,光电门测量位置和距转轴O的高度差h可以调节,有一质量为m的小球套在光滑杆上,重力加速度g取10m/s2.
(1)若杆的质量忽略不计,小球固定在杆OA的中点处,由静止释放杆,请写出光电门测量到的速度vA与高度差h的关系式;
(2)实际情况下杆的质量M不能忽略,拿走小球后重复实验,得到了如图所示的vA2与h关系图线.请写出杆绕O点转动时的动能Ek与vA的关系式;
(3)将光电门安装在OA中点正下方处,将杆由水平位置静止释放,套在杆上某处的小球由静止开始沿杆下滑,恰好经过该光电门,测得小球对地速度大小为v.已知杆的质量M是小球质量m的倍,杆绕O点转动时的动能Ek与vA满足(2)问关系.求此时小球重力做功的瞬时功率P.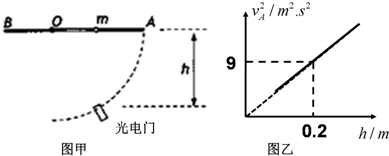
(1)根据图中几何关系可知,A端下降高度为h时,小球下降高度为,设此时小球的速度为v1.有机械能守恒定律:mv12=mg
由小球与A端共轴,有相同的角速度,所以:vA=2v1
解得:vA=2
(2)考虑杆的质量,拿走小球后,杆的重心距转轴O的距离为.因此杆的重心下降高度H与A端下降高度h的关系为:H=
对杆和球组成的整体,由动能定理得:Ek=Mg-Mg
由图象得:h=
得:Ek=
(3)小球下降高度h′=,此时杆与水平方向夹角为45°.由几何关系知,杆的重心下降高度H′=cos450=
设杆此时动能为Ek,小球垂直杆方向的分速度为v1,小球沿杆方向分速度为v2
杆和小球组成的系统机械能守恒:mg+Mg=mv2+Ek
解得:Ek=mgL-mv2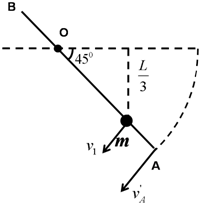
又:==,
Ek==
解得:v1=
又v2==
又:p=mgv1cos450+mgv2cos450
解得:p=10m()
答:(1)光电门测量到的速度vA与高度差h的关系式为vA=2;
(2)杆绕O点转动时的动能Ek与vA的关系式为Ek=;
(3)此时小球重力做功的瞬时功率P为10m().


