问题
解答题
小伟遇到这样一个问题,如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O。若梯形ABCD的面积为1,试求以AC,BD,AD+BC的长度为三边长的三角形的面积。
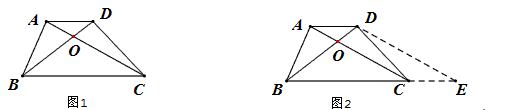
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可。他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题。他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2)。参考小伟同学的思考问题的方法,解决下列问题:
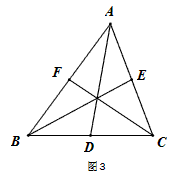
如图3,△ABC的三条中线分别为AD,BE,CF。
(1)在图3中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹);
(2)若△ABC的面积为1,则以AD,BE,CF的长度为三边长的三角形的面积等于_______。
答案
解:△BDE的面积等于1;
(1)如图,以AD、BE、CF的长度为三边长的一个三角形是△CFP;
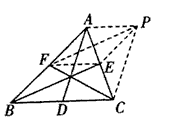
(2)以AD、BE、CF的长度为三边长的三角形面积等于 。
。
多项选择题 案例分析题
