问题
问答题
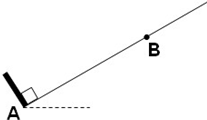
如图,一物块以150J的初动能从斜面底端A沿斜面向上滑动,到B时动能减少90J,机械能减少30J.
求:(1)第一次到达最高点时的重力势能为多少?(取斜面底端为零势点)
(2)若回到A时和挡板相碰无能量损失,物块运动过程中通过的总路程为多少?(设物块质量为1kg,斜面倾角为30°,g=10m/s2)
答案
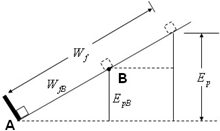
(1)设斜面倾角为θ,物体上滑s的位移,
摩擦力做功为Wf=-μmgscosθ=-μmgL(L为s在水平方向上的投影)
重力势能增加Ep=mgh
则
=μ|Wf| Ep
=μcotθ,当斜面倾角不变时,摩擦力做的功与重力势能增量的比值一定.L h
设从A点到最高点,摩擦力做功为Wf,在最高点重力势能为Ep
物体从A到B由动能定理得 WfB+WGB=△Ek
WfB=△E机
由题意得△Ek=-90J,△E机=-30J,联立得EpB=60J
则有
=|Wf| Ep
=|WfB| EpB 1 2
从A点到最高点由动能定理,有|Wf|+Ep=150,联立解得Ep=100J
(2)由(1)知μcotθ=
=|WfB| EpB
,则μ=1 2 3 6
因为mgsin30°>μmgcos30°,因此物体最终会停在挡板处,设总路程为S总,则由动能定理,得
-μmgS总cos30°=0-Ek0,
解得S总=60m
答:(1)第一次到达最高点时的重力势能为100J.
(2)若回到A时和挡板相碰无能量损失,物块运动过程中通过的总路程为60m.
