问题
问答题
设
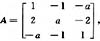 求A的特征值,并讨论A是否可对角化可对角化时写出对角矩阵。
求A的特征值,并讨论A是否可对角化可对角化时写出对角矩阵。
答案
参考答案:[*]
于是A的3个特征值为λ1=1-a,λ2=a,λ3=1+a
①当a≠0,且a≠[*]时,A有3个不同特征值,故A可以对角化,且可对角化为
[*]
②当a=0时,λ1=1,λ2=0,λ3=1,此时A有二重特征值1,而r(E-A)=2,λ1=λ3=1仅对应1个线性无关的特征向量,故此时A不可对角化。
③当[*]此时A有二重特征值[*]而[*][*]仅对应1个线性无关的特征向量,故此时A不可对角化。
