已知列向量组α1,α2,…,αs线性无关,列向量组β1,β2,…,βt可由α1,α2,…,αs线性表示,且
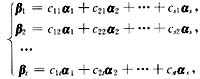
记矩阵C=(cij)s×t,证明:向量组β1,β2,…,βt线性相关的充分必要条件为矩阵C的秩r(C)<r。
参考答案:由题设,有
[*]
=(α1,α2,…,α3)C,
其中矩阵C的第j列是βj由α1,α2,…,αs线性表示的表示系数(j=1,2,…,t)。
必要性 因为β1,β2,…,βt线性相关,所以存在不全为零的数x1,x2,…,xt,使
x1β1+x2β2+…+xtβt=0,
记作
[*]
其中x=(x1,x2,…,xt)T≠0,于是有
(β1,β2,…,βt)x=(α1,α2,…,αs)Cx=0,
因向量组α1,α2,…,αs线性无关,故上式中α1,α2,…,αs的组合系数Cx只能为零,即
Cx=0
又x≠0,即上述齐次线性方程组有非零解,因此矩阵C的秩r(C)<t。
充分性 因为r(C)<t,因此存在x≠0,使Cx=0,因而有
(β1,β2,…,βt)x=(α1,α2,…,αs)Cx=(α1,α2,…,αs)·0=0,记x=(x1,x2,…,xt)T,则上式为
x1β1+x2β2+…+xtβt=0,其中x1,x2,…,xt不全为零,故向量组β1,β2,…,βt线性相关
解析:[评注] 若t>s,则r(C)<t,因此β1,β2,…,βt必线性相关;若t=s,则β1,β2,…,βt线性相关的充分必要条件为矩阵C的行列式|C|=0。
