问题
解答题
已知菱形ABCD的顶点A,C在椭圆x2+3y2=4上,对角线BD所在直线的斜率为1。
(1)当直线BD过点(0,1)时,求直线AC的方程;
(2)当∠ABC=60°时,求菱形ABCD面积的最大值。
答案
解:(1)由题意得直线BD的方程为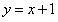
因为四边形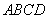 为菱形,
为菱形,
所以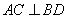
于是可设直线AC的方程为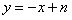
由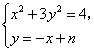 得
得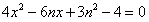
因为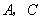 在椭圆上,
在椭圆上,
所以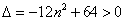 ,解得
,解得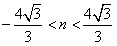
设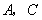 两点坐标分别为
两点坐标分别为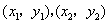 ,
,
则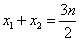 ,
,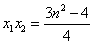 ,
,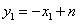 ,
,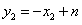
所以
所以AC的中点坐标为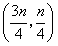
由四边形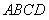 为菱形可知,点
为菱形可知,点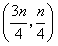 在直线
在直线 上,
上,
所以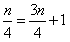 ,解得
,解得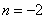
所以直线AC的方程为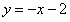 ,即
,即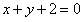 。
。
(2)因为四边形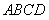 为菱形,且
为菱形,且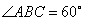 ,
,
所以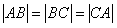
所以菱形 的面积
的面积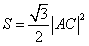
由(1)可得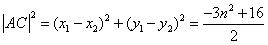 ,
,
所以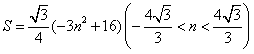
所以当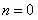 时,菱形
时,菱形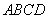 的面积取得最大值
的面积取得最大值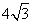 。
。
