问题
解答题
设直线l的方程为（a+1）x+y+2-a=0（a∈R）。
（1）若l在两坐标轴上的截距相等，求l的方程；
（2）若l不经过第二象限，求实数a的取值范围。
答案
解：（1）当直线过原点时，该直线在x轴和y轴上的截距都为零，截距相等，
∴a=2，方程即3x+y=0
若a≠2，由于截距存在，
∴
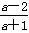=a-2，即a+1=1，
∴a=0，
方程即x+y+2=0。
（2）将l的方程化为（x+y+2）+a（x-1）=0（a∈R），
它表示过l1：x+y+2=0与l2：x-1=0的交点（1，-3）的直线系（不包括x=1）
由图象可知l的斜率-（a+1）≥0时，l不经过第二象限，
∴a≤-1。