问题
解答题
求过抛物线y=2x2-2x-1和y=-5x2+2x+3的交点的直线方程。
答案
解：联立方程组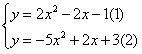
由（1）×5+（2）×2得6x+7y-1=0，
所以过抛物线y=2x2-2x-1和y=-5x2+2x+3的交点的直线方程为6x+7y-1=0。
搜题请搜索小程序“爱下问搜题”
求过抛物线y=2x2-2x-1和y=-5x2+2x+3的交点的直线方程。
解：联立方程组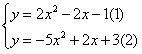
由（1）×5+（2）×2得6x+7y-1=0，
所以过抛物线y=2x2-2x-1和y=-5x2+2x+3的交点的直线方程为6x+7y-1=0。