问题
多选题
如图,两质量均为m的小球,通过长为L的不可伸长轻绳水平相连,从某一高处自由下落,下落过程中绳处于水平伸直状态.在下落h高度时,绳的中点碰到水平放置的光滑钉子O.重力加速度为g,空气阻力不计,则( )
A.小球从开始下落到刚到达最低点的过程中机械能守恒
B.从轻绳与钉子相碰到小球刚到达最低点的过程,重力的瞬时功率先增大后减小
C.小球刚到达最低点时速度大小为2g(h+L)
D.小球刚到达最低点时的加速度大小为(4h L+2)g 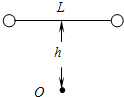
答案
A、小球从开始下落到刚到达最低点的过程中只有重力做功,机械能守恒,故A正确;
B、以向下为正方向,竖直方向合力为F=mg-Tsinθ,开始时θ很小,mg>Tsinθ,F>0,竖直方向加速度向下,vy增大,到快要相碰时,Tsinθ>mg,F<0,竖直方向加速度向上,vy减小,根据PG=mgvy可知重力的瞬时功率先增大后减小,故B正确;
C、从最高点到小球刚到达最低点的过程中运用动能定理得:
mv2=mg(1 2
+h),解得:v=L 2
,故C错误;2g(
+h)L 2
D、根据向心加速度公式有:a=
=v2 r
=(2g(
+h)L 2 L 2
+2)g,故D正确.4h L
故选ABD.
