水平固定的两根足够长的平行光滑杆AB和CD,两杆之间的距离为d,两杆上各穿有质量分别为m1=1kg和m2=2kg的小球,两小球之间用一轻质弹簧连接,弹簧的自由长度也为d.开始时,弹簧处于自然伸长状态,两小球静止,如图(a)所示.现给小球m1一沿杆向右方向的瞬时初速度,以向右为速度的正方向,得到m1的v-t图象为如图(b)所示的周期性图线(以小球m1获得瞬时速度开始计时).
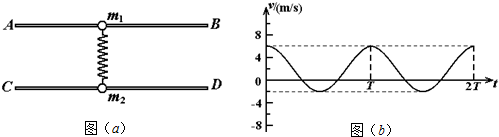
(1)求出在以后的过程中m2的速度范围;
(2)在图(b)中作出小球m2的v-t图象;
(3)若在光滑杆上小球m2右侧较远处还穿有另一质量为m3=3kg的小球,该小球在某一时刻开始向左匀速运动,速率为v=4m/s,它将遇到小球m2并与m2结合在一起运动,求:在以后的过程中,弹簧弹性势能的最大值的范围?
(1)以m1=1kg和m2=2kg组成的系统在相互作用过程中,水平方向动量守恒,所以
m1v0=m1v1+m2v2
解得:v2=v0-v1 2
当v1=6m/s时v2=0
当v1=2m/s时v2=2m/s
当v1=-2m/s时v2=4m/s
所以m2的速度范围是0≤v2≤4m/s
(2)所以一个周期内m2球的v-t图象如图所示:
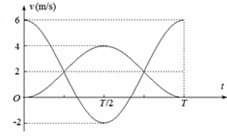
(3)设m2和m3碰撞后的速度是v23
m2v2-m3v=(m2+m3)v23
设m2和m3碰撞过程中机械能损失△E
△E=
m3v2+1 2
m2v22-1 2
(m2+m3)1 2 v 223
解得:△E=3(v2+4)2 5
当v2=0,损失的机械能最小,△Emin=9.6J
当v2=4,损失的机械能最大,△Emax=38.4J
当三个球的速度相同时,弹性势能最大,
根据动量守恒得m1v0-m3v=(m1+m2+m3)v共
解得:v共=-1m/s
整个相同具有的总机械能E总=
m1v02+1 2
m3v 21 2
设弹簧弹性势能的最大值是Ep,对全过程应用能量守恒定律得:
E总=
(m1+m2+m3)v共2+△E+Ep1 2
弹簧弹性势能的最大值Ep=39-△E
弹簧弹性势能的最大值的范围是0.6J~29.4J
答:(1)m2的速度范围是0≤v2≤4m/s
(2)如图
(3)弹簧弹性势能的最大值的范围是0.6J~29.4J
