Regardless of their political affiliation, in all countries women must overcome a host of stumbling blocks that limit their political careers. "Most obstacles to progress consist of (1) of various kinds," says the Inter-Parliamentary Union (IPU), a Geneva-based organization (2) 139 parliaments, including the lack of time, training, information, self-confidence, money, support, motivation, women’s networks and solidarity between women.
In every culture, prejudice and stereotypes (3) hard. The belief still holds (4) that women belong in the kitchen and (5) the children, not at election (6) or in the Speaker’s chair. The media often reinforce traditional images of women, who, upon entering politics, also bear the brunt (正面冲击) of verbal and physical (7) .
In impoverished (贫穷的) countries (8) by civil conflicts and deteriorating economic and social conditions, women are (9) by the tasks of managing everyday life and looking after their families.
The IPU stresses the general lack of child-care facilities—often (10) a privileged few—the (11) of political parties to change the times and running of meetings and the weak backing women receive from their families. That support, which is (12) as well as financial, is (13) vital because women have internalized (14) images of themselves since the (15) of time and often suffer from low self-confidence.
Another obstacle is the lack of financial resources, especially as election campaigns become increasingly expensive. (16) , women encounter more or less open machismo (男子汉的高傲) in the (17) of closed political circles (18) entry to the "second sex. " Lastly, they (19) the lack of solidarity between women, (20) by the fact that the number of available positions is limited.
5（）
A.with
B.to
C.among
D.into
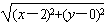）2=|x+2|2+12，
，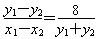